파이썬/머신러닝

[분류모델] 02. Decision Tree

토마토농장농장 2022. 5. 30. 16:45

Decision Tree (의사결정나무) :  변수들로 기준을 만들어 샘플을 분류하고 분류된 집단의 성질로 추정하는 모형

- 장점 : 해석력이 높음
- 단점 : 변동성이 높음(샘플이 조금만 추가되더라도 기준이 잘 바뀜)
 

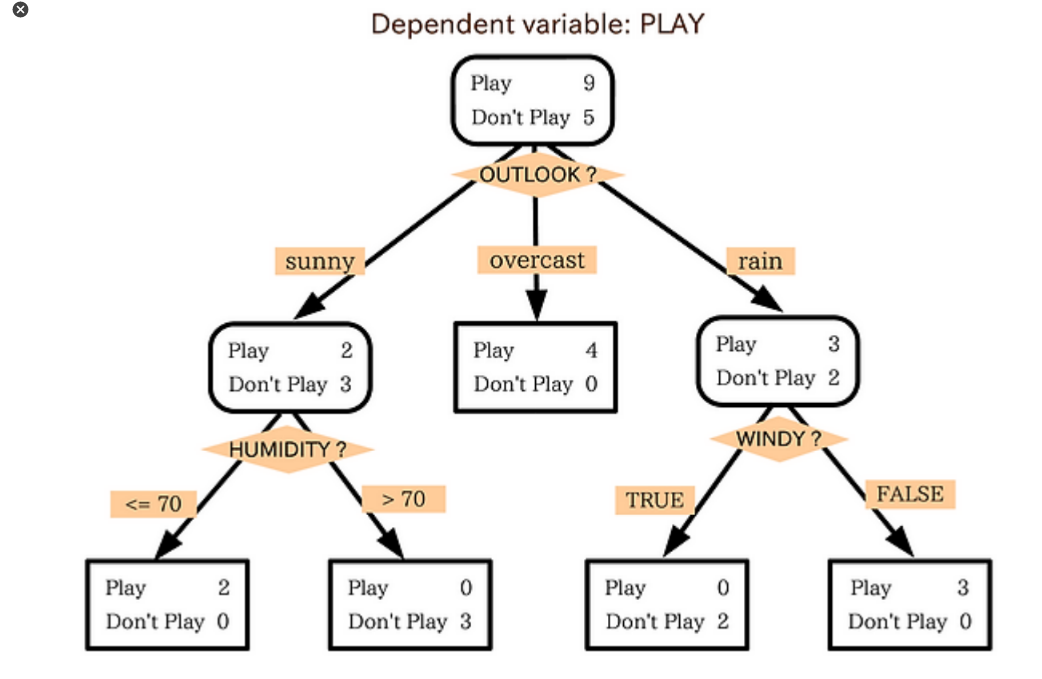
 종속변수의 종류가 범주형이면 분류, 수치형이면 회귀 분석을 이용한다. 

 

 

 

*Entropy 엔트로피 : 의사결정나무의 수학적인 개념.

엔트로피 함수는 아래와 같다. 

 
- 클래스가 2개인 데이터를 하나 뽑았을때 클래스 1이 나올 확률이 0.5일때 엔트로피값은 1을 갖는다. 잘 퍼져있다. 
- 엔트로피가 1이라는 의미는 데이터가 잘 섞여 있다는 의미
 
예를 들어 아래와 같이 모든 결과가 동일한 종속변수 값 'Yes'를 갖는다면, 엔트로피값은 한쪽에만 치우쳐있으므로 0이다. 
'Yes', 'No' 의 결과 수가 동일하다면 엔트로피는 1의 값을 갖는다. 

 

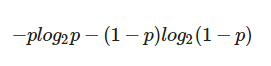
의사결정나무를 통과하기 전에는 엔트로피가 1이지만, 의사결정나무를 통과하게 되면 조건에 따라 종속변수가 종류별로 분리되므로 엔트로피는 0에 가까워진다.  엔트로피가 0에 가까울 수록 잘 분리됐다고 본다.  

 

 

 

 

Information Gain : 의사결정나무의 성능 체크

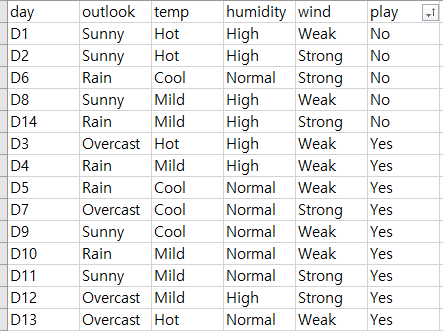
샘플 데이터가 위와 같다고 할 때, 의사결정나무를 통과하기 전의 Yes의 확률 p = 9/14 이다. 

엔트로피 공식에 넣으면, 

before_entropy = -(9/14) * np.log2(9/14) - (1 - (9/14)) * np.log2(1 - (9/14))
before_entropy

분기점을 통과하기 전의 엔트로피 값은 약 0.94가 나온다. 

 

첫번째 분기점을 지나고 난 후의 확률은 각각, 

Yes :4, Yes:2 NO: 3, Yes:3 No:2 으로 , 

1, 0.4, 0.6 이다. 

 

엔트로피는 각각 계산한 후, 가중평균을 이용해서 구한다.

 

 

after_entropy_1 = 0
after_entropy_2 = -0.4 * np.log2(0.4) - (1 - 0.4) * np.log2(1 - 0.4)
after_entropy_3 = -0.6 * np.log2(0.6) - (1 - 0.6) * np.log2(1 - 0.6)
after_entropy = (4 * after_entropy_1 + 5 * after_entropy_2 + 5 * after_entropy_3) / (4 + 5 + 5)

after_entropy_1,2,3은 각각 (0, 0.9709505944546686, 0.9709505944546686)

가중평균의 엔트로피 after_entropy = 0.6935361388961919

 

information_gain = before_entropy - after_entropy

 

[노드를 설정하는 방법]

  • information gain이 가장 높은 변수를 root 변수로 설정
  • 나머지 변수들을 information gain을 구하고 information gain이 가장 높은 변수를 다음 노드로 설정

 

 

 

 

 

 

 

 

[Iris 예제]

 

sklearn datasets에 내장되어있는 iris 데이터를 불러온다. 

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
iris = datasets.load_iris()

 

 

 

feature와 target 이 이미 나뉘어 있다. 

iris data를 보기 쉽게 데이터 프레임 형태로 변환하면,

import pandas as pd
df = pd.DataFrame(iris.data, columns=iris.feature_names)

 

 

target 값들은 나오지 않는데, target 컬럼을 아래와 같이 추가한다.  

df['label'] = iris.target
df.tail()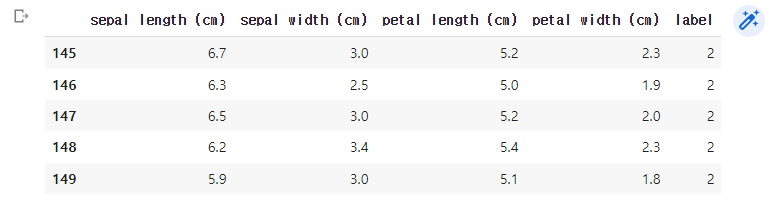

 

 

 

[모델의 학습]

model = DecisionTreeClassifier(max_depth=2, random_state=1).fit(iris.data, iris.target)

max_depth :  몇번 분할할 것인지. 너무 많이 분할하면 overfitting 된다. 

 

 

 

 

 

[모델 시각화]

 

from sklearn.tree import export_graphviz
export_graphviz(model, out_file="tree.dot", class_names = iris.target_names, 
                           feature_names = iris.feature_names, impurity=True, filled=True)
import graphviz
# 위에서 생성된 tree.dot 파일을 Graphiviz 가 읽어서 시각화
with open("tree.dot") as f:
    dot_graph = f.read()
graphviz.Source(dot_graph)

※ 지니계수 : 불순도를 나타내는 지표. value = [ ] 로 주어진 데이터 분포에서의 지니계수.  

 

 

 

 

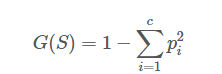
[모델 평가]

Confusion Matrix 

 

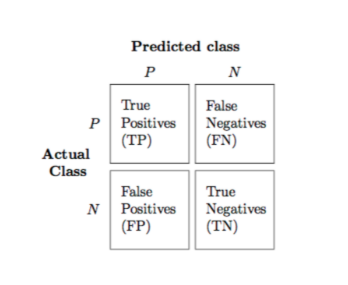
True Positives : 1인 레이블을 1이라 하는 경우를 True Positives라고 한다. -> 관심 범주를 정확하게 분류한 값.

False Negatives : 1인 레이블을 0이라 하는 경우를 False Negatives라고 한다. -> 관심 범주가 아닌것으로 잘못 분류함.

False Positives : 0인 레이블을 1이라 하는 경우를 False Positives라고 한다. -> 관심 범주라고 잘못 분류함.

True Negatives : 0인 레이블을 0이라 하는 경우를 True Negatives라고 한다. -> 관심 범주가 아닌것을 정확하게 분류.

 

TP/ TN 이 높고 FN/FP가 낮은게 좋음. 

from sklearn.metrics import confusion_matrix
confusion_matrix(iris.target, model.predict(iris.data))

디시전트리에 의한 TP값은 49, TN은 45이다. 

 

 

model.score(iris.data, iris.target)

 

저작자표시 (새창열림)